개념
최소자승법은 데이터를 가장 잘 설명할 수 있는 직선(또는 곡선)을 찾는 방법입니다.
예를 들어,
어떤 가계에서 일주일 동안 하루하루 아이스크림이 몇 개나 팔렸는지 기록이 있다고 생각해 봅시다.
이 데이터를 보면 어떤 날은 많이 팔리고, 어떤 날은 조금 팔리고 해서 숫자가 들쭉날쭉 할 텐데요.
이 아이스크림 판매량이
전반적으로 증가하는지, 감소하는지, 또는 그냥 비슷하게 유지되는지 알고 싶은 경우
최소 자승법을 사용하면 데이터를 가장 잘 설명할 수 있는 "최적의 직선"을 찾을 수 있습니다.
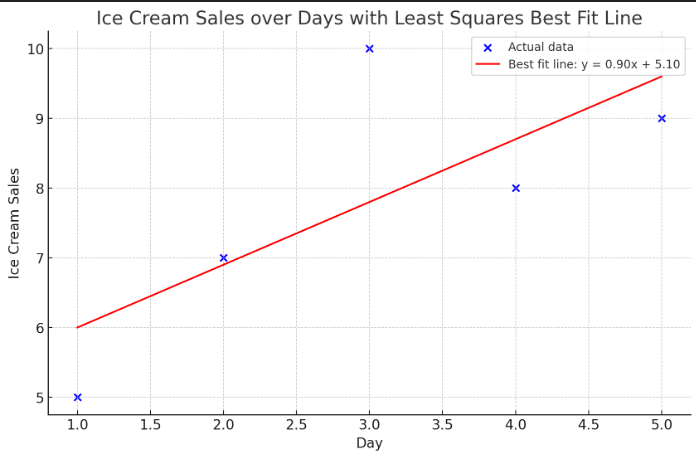
파란색 점은 각 요일의 실제 아이스크림 판매량을 나타내고,
빨간색 선은 최소 자승법을 통해 구한 "최적의 직선"입니다.
그래서 그래프를 해석하면 아이스크림 판매량이 전반적으로 증가하고 있다고 봐도 될 거 같죠?
세부내용
x가 날짜를 나타내고, y가 팔린 아이스크림 개수, 그리고 목표는 y = ax + b 형태의 최적의 직선을 찾는다는 것을 가정해 봅니다. 그럼 우리의 목표는 최적의 a, b 값을 찾아내는 거라고 할 수 있겠죠?
위 파란색 5개의 점을 아래와 같이 표현할 수 있을 것입니다.
(x1, y1) = (1, 5)
(x2, y2) = (2, 7)
(x3, y3) = (3, 10)
(x4, y4) = (4, 8)
(x5, y5) = (5, 9)
이를 행렬로 표현하면 다음과 같이 표현할 수 있겠죠?


이 식을 간단히 나타내보면 아래와 같이 표현할 수 있는데요.
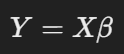
우리가 구하고 싶은 부분은 β입니다.
행렬식으로 β 값을 구하기 위해 식을 전개해 보면 다음과 같이 표현할 수 있습니다.
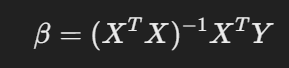
이 공식을 통해 β를 구하면 a, b 값을 얻을 수 있습니다.




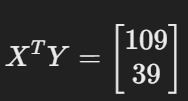

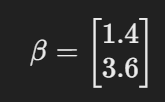
따라서 데이터를 가장 잘 설명하는 직선의 방정식은
y = 1.4x + 3.6이라 할 수 있겠습니다.
최소 자승법의 한계
선형 관계 가정
최소자승법은 선형 관계를 따른다고 가정합니다. 따라서 비선형적 패턴(곡선, 지수증가 등)을 보이는 경우 잘 설명할 수 없게 됩니다. 이런 경우는 비선형 회귀분석 등을 사용하여 비선형 관계를 모델링할 수 있어요
이상치에 민감
최소 자승법은 오차를 제곱하여 합산하는 방식이기 때문에,
극단적으로 큰 오차(이상치)에 매우 민감합니다.
하나의 이상치가 전체 회귀 직선의 방향을 크게 바꾸어 결과를 왜곡할 수 있어요.
이런 경우 이상치를 제거하거나 Robust Regression과 같은 이상치에 덜 민감한 방법을 사용하거나 오차의 절댓값을 합산하는 절대 편차 최소화 같은 다른 방법도 고려해 볼 수 있습니다.
변수 독립성 가정
최소 자승법을 사용할 때 독립 변수들 간에 상관관계가 높으면 (다중공선성) 정확한 계수를 추정하기 어렵습니다.
예를 들어, 두 개 이상의 독립변수가 매우 유사한 값을 가지면, 계수 추정치가 불안정해지고 모델이 신뢰할 수 없는 결과를 낼 수 있습니다.
이외 여러 한계점들을 이해하고 데이터 특성과 상황에 맞게 최소자승법을 보완하여 사용하는 것이 중요하겠습니다.
'Data Science > Algorithm' 카테고리의 다른 글
| 특이값 분해 (Singular Value Decomposition, SVD) (1) | 2024.11.18 |
|---|---|
| RAG (Retrieval-Augmented Generation) (1) | 2024.11.16 |
| Contextual Bandit & LinUCB (0) | 2024.11.14 |
| Multi-Armed Bandit (MAB) (4) | 2024.11.13 |
| Deep Cross Network (0) | 2024.11.11 |



댓글